红黑树

• 概述

红黑树是一种自平衡二叉搜索树 (任意节点的左子树的值均小于该节点，任意节点右子树的值均大于该节点，在插入删除节点后自动调整树的结构保证树的高度平衡，即任意节点的左右子树高度差不大于1) , 红黑树的节点会有颜色区分，不是红色就是黑色。

1. 叶子结点*(没有子结点的节点)*、根结点、空节点为黑色
2. 红色结点的子结点为黑色
3. 任意节点到叶子结点所有路径上的黑色结点数目一致

• 操作

• 旋转

为保证二叉树平衡，在插入删除节点后可能会通过旋转操作保持平衡。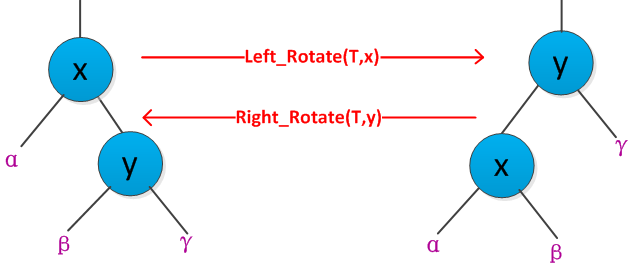

• 插入

红黑树插入一个新结点的过程RB_INSERT是在二叉查找树插入过程的基础上改进的，先按照二叉排序的插入过程插入到红黑树中，然后将新插入的结点标记为红色，然后调用一个辅助的过程RB_INSERT_FIXUP来调整结点并重新着色，使得满足红黑树的性质。

• 删除

红黑树删除结点过程是在二叉查找树删除结点过程的基础改进的。与二叉查找树类似，删除的结点分为三种情况：

1. 无左右孩子
2. 有左孩子或者右孩子
3. 既左孩子又有右孩子

红黑树在删除结点后需要检查是否破坏了红黑树的性质。如果删除的结点y是红色的，则删除后的树仍然是保持红黑树的性质，因为树中各个结点的黑高度没有改变，不存在两个相邻（父结点和子结点）的红色结点，y是红色不可能是根，所有根仍然是黑色。如果删除的结点z是黑色的，则这个是破坏了红黑树的性质，需要调用RB_DELETE_FIXUP进行调整。从删除结点y的唯一孩子结点x或者是NIL处开始调整。

• ref

红黑树详解